[EECS 498-007] Lecture 2. Image Classification

본 포스팅은 CS231n의 업데이트 버전인 EECS 498-007 / 598-005 강의를 듣고 요약한 것입니다.

Image Classification

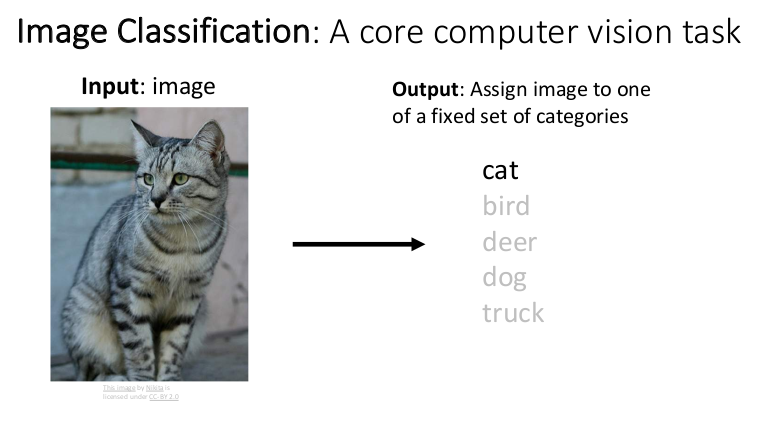
이미지 분류(Image Classification)는 입력된 이미지를 사전에 정해둔 몇 가지 카테고리 중 하나로 분류하는 작업이다. 인간은 직관적으로 이미지를 인식하고 판단할 수 있지만 컴퓨터는 하나의 이미지를 거대한 숫자 배열(가로 픽셀 X 세로 픽셀 X 색상 채널)로 표현한다. 컴퓨터가 이미지를 직관적으로 인식하지 못하기 때문에 이미지 분류를 하기 위해 극복해야 할 여러 가지 문제들이 존재한다.

• Viewpoint Variation: 같은 사물이라도 사진을 찍는 방향에 따라 다르게 보인다.
• Intraclass Variation: 같은 카테고리 내의 사물이라도 생김새가 모두 다르다.
• Fine-Grained Categories: 한 카테고리에 내에서도 종류별로 미세한 차이가 있다.
• Background Clutter: 배경색과 사물의 색이 비슷하면 구분하기 어렵다.
• Illumination Changes: 조명의 변화에 따라 사물이 다르게 보인다.
• Deformation: 사물의 모습이 변형되는 경우도 있다.
• Occlusion: 사물이 가려져 일부만 보이는 경우도 있다.

 

이미지 분류는 종양의 악성 여부 판단처럼 그 자체로도 유용하게 쓰일 수 있지만, 컴퓨터 비전의 여러 과제에 활용되기도 하는 가장 핵심적인 기술이다.

• Object Detection: 이미지에서 특정 사물을 인식해내는 기술
• Image Captioning: 이미지를 설명하는 문장을 만들어내는 기술
• Playing Go: 바둑에서 다음 수를 둘 위치 결정하는 기술

 

 

Machine Learning: Data-Driven Approach

특정 대상을 인식하여 분류하는 알고리즘을 직접 작성하는 명확한 방법은 없다. 따라서 수많은 데이터를 주고 컴퓨터를 학습시키는 데이터 기반 접근법(Data-Driven Approach)을 사용한다. 이미지를 수집하여 라벨링을 하고, 머신러닝 기법으로 분류 모델을 학습시키고, 새로운 이미지를 활용해서 모델의 성능을 평가하는 방법이다. 분류 대상이나 카테고리를 변경하더라도 새로운 데이터셋으로 훈련시키기만 하면 되는 것이다. 데이터 기반 접근법을 사용하려면 많은 데이터가 필요한데, 이미지 분류에 쓰이는 대표적인 데이터셋에는 MNIST, CIFAR10, CIFAR100, ImageNet, MIT Places, Omniglot 등이 있다.

 

 

Nearest Neighbor

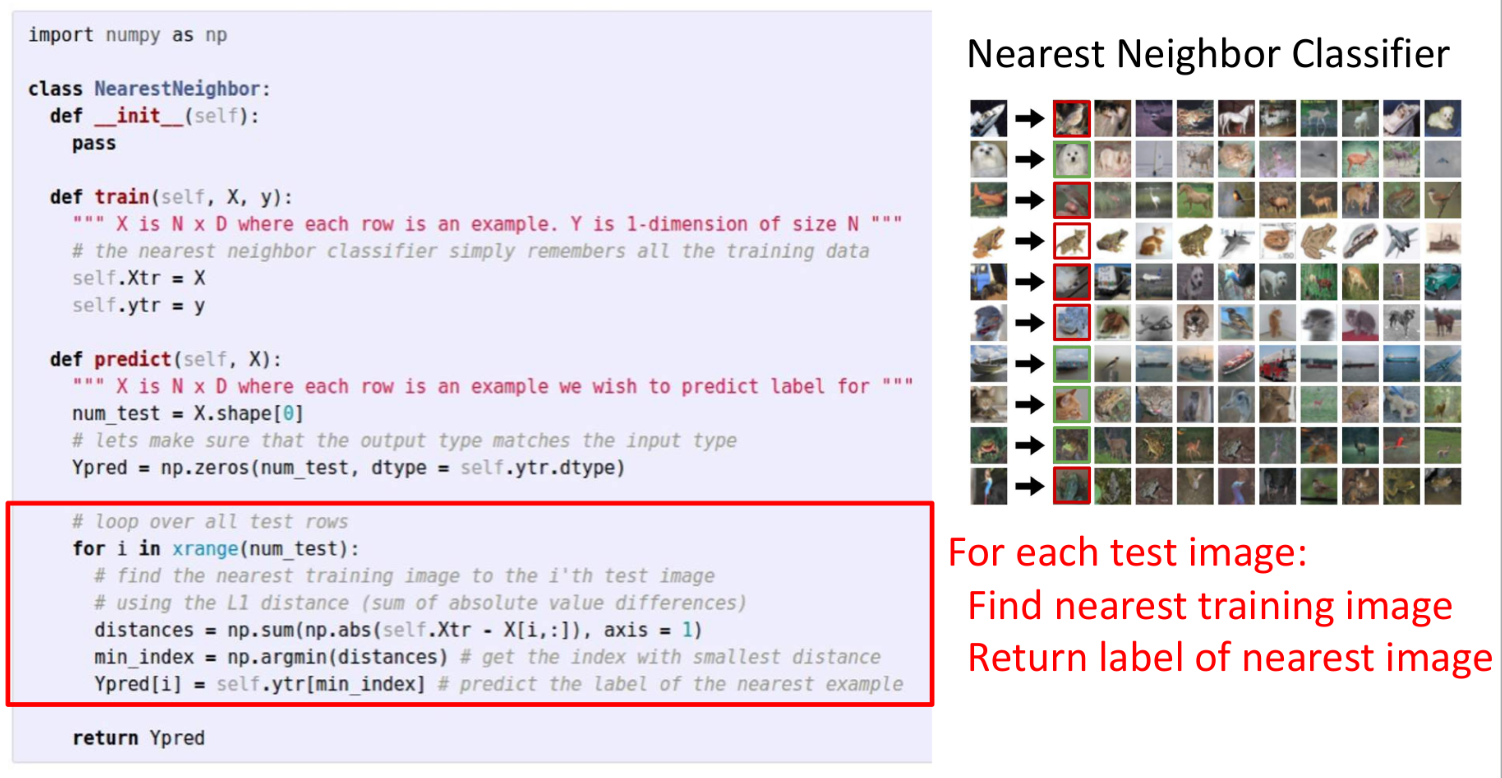
Nearest Neighbor는 가장 간단한 이미지 분류 알고리즘으로, 모든 트레이닝 데이터를 암기한 다음 테스트 이미지와 가장 유사한 트레이닝 이미지를 찾아 분류하는 방식이다. 유사도를 계산하기 위해 각 픽셀값의 거리를 측정하는데, 이때 사용되는 거리 측정법 중 하나가 L1 거리(L1 distance)이다. 각 픽셀별로 차이를 구해 절댓값을 취한 값을 모두 더하는 방법이다.

 

이 알고리즘의 시간 복잡도를 살펴보면, 훈련 과정은 모든 트레이닝 데이터를 단순히 카피하면 되므로 상수 시간(O(1))이 소요된다. 반면 테스트 과정은 테스트 데이터를 모든 트레이닝 데이터와 일일이 비교해야 하므로 데이터 개수 N에 비례하는 선형 시간(O(N))이 소요되어 속도가 매우 느리다. 그리고 오른쪽 그림처럼 단순히 색과 모양이 비슷한 이미지를 유사하다고 판단하기 때문에 실제 대상을 제대로 분류하지 못한다는 단점이 있다.

 

 

K-Nearest Neighbors

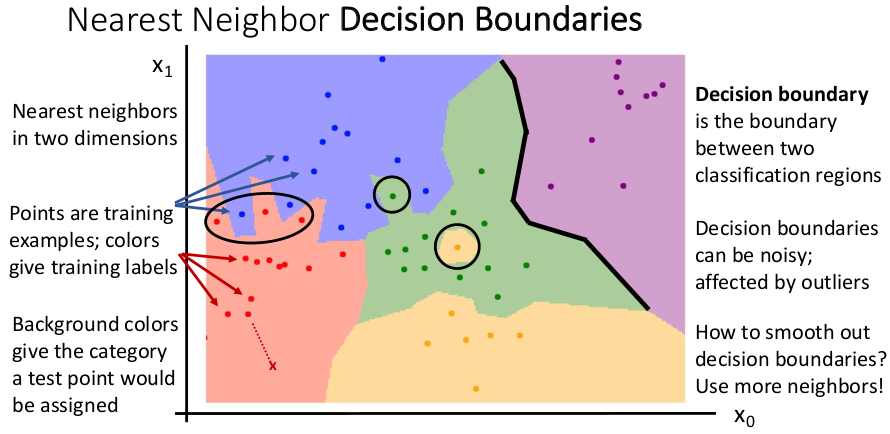
Nearest Neighbor 분류를 시각화한 위 그림에서 각각의 점들은 트레이닝 데이터셋이고 배경색은 카테고리를 나타낸다. 예를 들어 빨간색이 고양이고 파란색이 개라면, 주어진 테스트 데이터 X는 빨간색 영역에 있으므로 고양이로 분류된다. 그런데 각 영역의 경계선이 빨간색과 파란색의 경계처럼 복잡해지거나, 초록색 안에 노란색이 박혀있는 것처럼 이상치의 영향을 받는 경우가 생긴다.

 

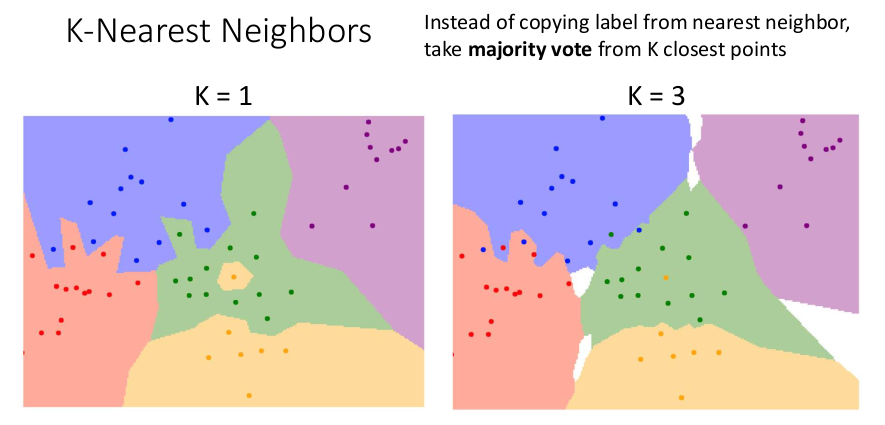
결정 경계(Decision Boundaries)를 매끄럽게 만드는 방법은 이웃의 수를 1개가 아닌 K개로 늘리고 다수결 투표로 카테고리를 결정하는 것이다. K개의 이웃을 사용하므로 이러한 알고리즘을 K-Nearest Neighbors라고 한다. K = 3일 때를 보면 K = 1일 때보다 경계가 부드럽고 이상치의 영향이 줄었다. 하지만 K가 1보다 커지면 그림의 흰색 영역처럼 모든 카테고리가 동점을 이뤄 어느 쪽으로도 분류되지 않는 부분이 생겨난다.

 

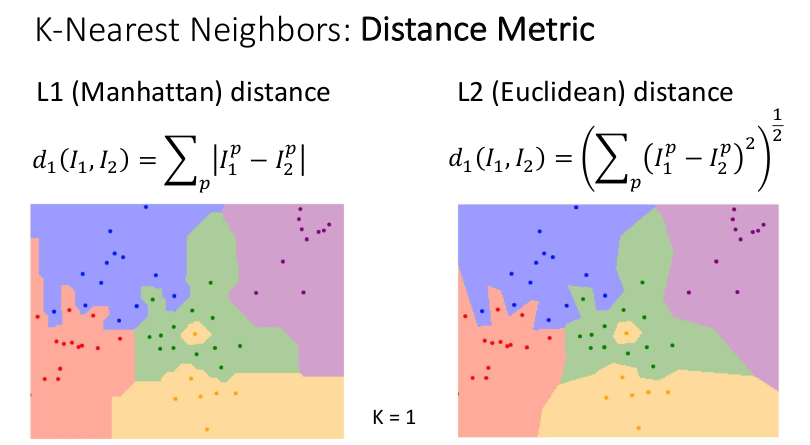
또 다른 해결 방법은 거리 측정법(Distance Metric)을 바꿔보는 것이다. 차이의 절댓값인 L1 (맨해튼) 거리 대신, 차이의 제곱에 루트를 씌운 L2 (유클리드) 거리를 사용하면 결정 경계가 좀 더 반듯해진 것을 볼 수 있다. 둘 중 어느 것이 더 좋다고 단정지을 순 없지만, 적절한 거리 측정법을 사용하면 다양한 유형의 데이터에 K-Nearest Neighbor를 적용할 수 있다. 예를 들면 tf-idf 유사성을 이용해 유사한 논문 찾는 것처럼 텍스트 데이터에도 활용이 가능하다.

 

 

Hyperparameters

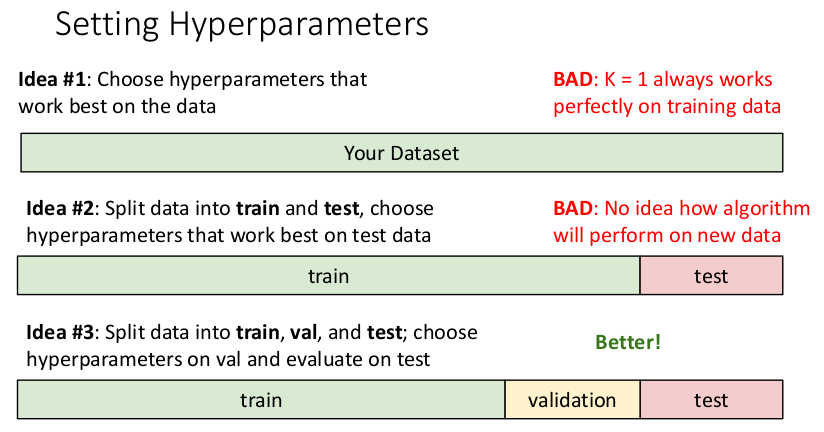
하이퍼파라미터(Hyperparameters)란 K값이나 거리 측정법처럼 학습 알고리즘에서 선택할 수 있는 부분이다. 하이퍼파라미터는 알고리즘의 근본적인 작동 방식과 관련이 있기 때문에 트레이닝 전에 미리 설정해야 하며, 트레이닝 데이터 학습을 통해 값을 구할 수 없다. 하이퍼파라미터 설정에 따라 결과가 달라지므로 여러 가지 값이나 방식을 적용해보고 가장 적절한 것을 선택해야 한다.

• Idea #1: 전체 데이터셋에 대해 가장 높은 정확도를 보이는 값을 선택한다. → 트레이닝 데이터에는 항상 100%의 정확도를 보이지만 다른 데이터에는 적용되지 않는다.
• Idea #2: 데이터를 훈련용(train)과 테스트용(test)으로 나눠 테스트 데이터에 가장 잘 맞는 값을 선택한다. → 하이퍼파라미터 설정에 테스트 데이터가 이미 사용되었으므로 새로운 데이터에 대해 어떤 성능을 보일지 알 수 없다.
• Idea #3: 데이터를 훈련용(train), 검증용(validation), 테스트용(test)으로 나눠 검증용 데이터에 가장 잘 맞는 값을 선택하고 마지막에 테스트 데이터로 평가한다. → 1, 2보다 나은 방법
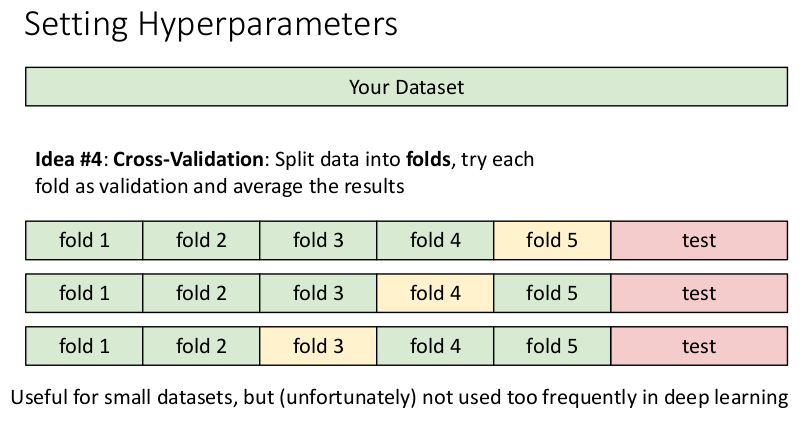
• Idea #4: 교차 검증(Cross-Validation)
  데이터를 여러 개의 덩어리(fold)로 분할하고, 각 fold를 검증용 데이터로 사용하여 검증을 반복하며 최적의 값을 선택한다. → 가장 이상적인 방법. 특히 데이터 수가 적을 때 유용하다.

 

 

K-Nearest Neighbor on raw pixels is seldom used

트레이닝 데이터의 수가 무한히 많아지면 K-Nearest Neighbor로 어떤 함수든 나타낼 수 있다(Universal Approximation). 그러나 트레이닝 데이터의 모든 부분을 고르게 커버하려면 트레이닝 포인트가 매우 많이 필요하다. 차원이 증가함에 따라 트레이닝 포인트는 기하급수적으로 증가하게 되고, 데이터 사이에 빈 공간이 생겨 모델의 성능이 저하되는 차원의 저주(Curse of Dimensionality)가 발생한다.

이번 강의에서 배운 K-Nearest Neighbor를 이미지의 원시 픽셀에 적용하는 방식은 오늘날 거의 사용되지 않는다. 테스트 속도가 매우 느리고, 픽셀 간의 거리가 이미지에 대한 유용한 정보를 표현하지 못하기 때문이다. 아래 이미지에서 가장 왼쪽의 원본 이미지와 비교했을 때, 다른 이미지 3개 모두 L2 거리가 동일하다. 시각적으로는 세 번째 이미지(Shifted)가 원본과 가장 유사하지만, 거리값에 이러한 정보가 반영되지 않으므로 별 의미가 없는 것이다. 대신 컨볼루션 신경망(ConvNet)을 통해 이미지의 특징(features)을 추출하여 Nearest Neighbor 알고리즘을 적용하는 방법이 널리 사용되고 있다.